| Problem | Solution |
|---|---|
 |
  
Symmetry: None
|
 |
    |
 |
       |
 |
   |
 |
  |
 |
       |
 |
    |
 |
         |
 |
   |
 |
     |
 |
 |
 |
  |
 |
  |
 |
  |
 |
   |
 |
     |
 |
    |
 |
 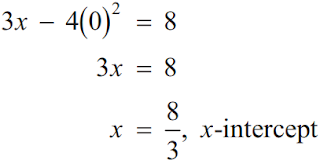   |
13 Insanely Easy Techniques to Hack & Exploit Agentic AI Browsers
-
Agentic AI browsers (e.g., Microsoft Copilot in Edge, OpenAI’s “agent mode”
sandboxed browser, and Perplexity’s Comet) are designed to autonomously
brows...
6 days ago








0 comments:
Post a Comment